| swiss-algebra-help.com |
 |
|
Proportional Reasoning
Many aspects must be taken into consideration: cognitive functions, concrete activities, intuition, abstract intelligence, quantitative reasoning (see picture on the left-hand side) [1]. Susan J. Lamon, in her book [1], stresses the importance of getting to work on fractions without pre-given algorythm but rather through practical exercises. And leave the children work out their solutions and understanding. The book is full of practical examples and activities to enhance the understanding of fractions. It also points out some common misconception about fractions (e.g. a "fraction" in our daily life is often understood as a "tiny portion" of something, so what about the fraction 10/7 - an improper fraction- which is bigger than the unity, uh?). Moreover, the use of a single pizza in many exercises tends to make children believe that "unity" means a single object. That's why unitizing is so important: Check this example taken from the book. What is the fraction in the figure below?
The answer could be 5 (each circle is a unit), 2 1/2 (each column is a unit), 5/8 or 3/8 (depending wheter you consider the yellow or white circles, and provided you see 8 circles as the "whole"), 1 1/4 (a unit is 4 circle). So it's very important that children learn to ask: what is unit?
Moreover, proportional reasoning can be of two types: direct proportions (if I increase a value, then another value increases) indirect proportions (if I increase a value, then another value decreases) I have seen in a math forum a mother asking for help for her 11 years old daughter about a ratio problem (see in my fraction worksheets webpage, the first problem -"The sea or the mountain?") and eventually get the result...by a "smart" guy and through an algebraic equation her daughter could not possibly understand since she had no knowledge of it. That's what , in my opinion, teaching should be all about: to help provide the tools for fishing, not the fish itself. Conclusion
Source: 1. Teaching Fractions And Ratios For Understanding: Essential Content Knowledge And Instructional... From proportional reasoning back to basic algebra fractions homepage
|
On the shore of a vast sea
|
|
|
Stay in touch with nature. It's full of mathematics! 
Enjoy This Site?
Then why not use the button below, to add us to your favorite bookmarking service? |
||
|
| Homepage| About Us |Study Tips |Contact | This Website is Powered by Site Build It! - and I would never use anything else.
|
||
|
| ||
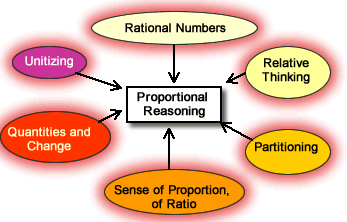 Proportional reasoning is built over time.
Proportional reasoning is built over time. 
