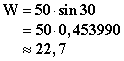Trigonometry in Geology

An example of applied trigonometry in geology:

How to find the real width of a geological bed

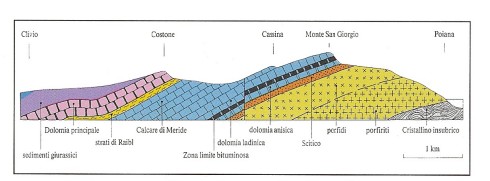
Look at the picture here on the left. Now we are about 20 kilometers (13 miles) North from the picture of the homepage and looking at the same two mountains but facing South...

On the right-hand side of the picture is Mount San Giorgio (the people swimming underneath are my children and my wife). On the left hand-side is Mount Generoso (a Mesozoic to Cenozoic oceanic deposit).

Mount San Giorgio is quite famous for his Triassic fossils and its geology is fairly well known.

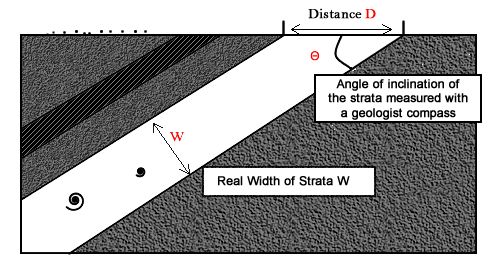
Now we simplify the geology for educational purposes.

A geologist can measure the distance D of an outcropping strata and its inclination - which is the angle or "how steep" the layer is "going down" - (a geologist uses a simple geologist compass which is alway equipped with a clinometer).
Yet, measuring that length D of the outcrop doesn't correspond to know the real thickness of the strata W (see below). So we want to find out what is the real width of the strata.

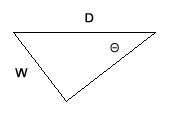
As we said, the real width or thickness of the strata W can be simply derived by fields measurement of D (using a meter or just by counting the footsteps) and Θ (using a geologist compass ).

In fact, trigonometry enshrine "secret" natural rules which bind those three units : W, D, Θ.

In other words, we can imagine that D and W are the sides of a right triangle, and Θ is one angle of it (see the picture below).

The Greek astronomers found out that the relation which binds those 3 things (D, W,Θ) in a right triangle is universal (i.d. valid in all universe, yes) and indipendent from the size of the triangle!

And the relation is:

Now, "sinΘ" is just an "intelligent proportion" - a number - going from 0 to 1.

From algebra, you will know that the above relation can also be written as

Now, let's say we measured Θ = 30º and D=50 meters, then we have

So the solution of our "trigonometry in geology" example is that the real strata is about 22,7 meters wide.

From Trigonometry in geology back to the homepage

Source:
http://www.montesangiorgio.ch/geologia.htm
http://whc.unesco.org/en/list/1090