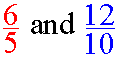swiss-algebra-help.com

Equivalent Fractions

$Equivalent fractions illustration as you dressing up in a costume:it's still you but you look differently!$

Equivalent fractions are...Like when you dress up in a costume!
You look different but It's is still you in the end!

When two or more fractions express the same value ( the same ratio ) but are written in a total different way, then they are called equivalent!

for example

. $equivalent fractions$

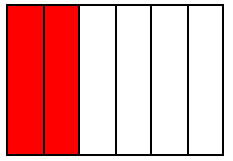
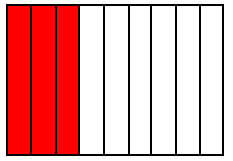
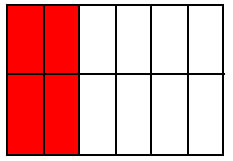
Another way to look at it is to consider areas.

Like in the following example, the red area stay the same (keep the same value) but the fraction changes because the unit changes: 3 parts, 6 parts, 9, parts, 12 parts....

$equivalent fraction 1$	1/3	original partitions (3) Denominator=3 Numerator (red area) = 1 partition
$equivalent fraction 2$	2/6	2 times the original partions (6) Denominator=6 Numerator (red area) = 2 partitions
$equivalent fraction 3/9$	3/9	3 times the original partions (9) Denominator=9 Numerator (red area) = 3 partitions
$equivalent fraction 3$	4/12	4 times the original partions (12) Denominator=12 Numerator (red area) = 4 partitions

Another way to recognize equivalent fraction is when you are reducing them: you want to make their numbers smaller so that it's easier to "carry them along" when solving a practical problem.

In the end is easier to cut a piece wood in 1/3 than in 3245/9735, isn't it?

Did you notice? In the above fraction, 3245/9735, the Greatest Common Factor (GCF) is...3245!

514. A superficial knowledge of mathematics may lead to the
belief that this subject can be taught incidentally, and that ex-
ercises akin to counting the petals of flowers or the legs of a
grasshopper are mathematical. Such work ignores the funda-
mental idea out of which quantitative reasoning grows the
equality of magnitudes. It leaves the pupil unaware of that
relativity which is the essence of mathematical science. Nu-
merical statements are frequently required in the study of nat-
ural history, but to repeat these as a drill upon numbers will
scarcely lend charm to these studies, and certainly will not
result in mathematical knowledge. SPEER, W. W.

Primary Arithmetic (Boston, 1897), pp. 26-27.

source: Memorabilia mathematica; or, The philomath's quotation-book - Moritz, Robert Édouard, 1868-1940

Greatest Common Factor Calculator

Least Common Multiple Calculator

Adding Fractions

Subtracting Fractions

Multiplying fractions

Dividing Fractions

From equivalent fractions back to basic algebra fractions